 Dit artikel is meer dan 10 jaar geleden geschreven en sluit aan bij twee artikelen in ESB in 1989 en 1990. Beide artikelen waren coproducties met Dr J.M.G. Frijns die de modellering verzorgde. Het was de periode dat binnen het APB de eerste inzichten rond ALM ontwikkeld werden. In het 1989 artikel lieten we zien dat een optimale allocatie onafhankelijk is van het inflatie niveau1 . In het 1990 artikel lieten we zien hoe het systeem van premieaanpassing van invloed is op het gedrag van de dekkingsgraad in de tijd2. Het derde artikel was bedoeld als overzichtsartikel voor de Amerikaanse/Engelse lezer maar ging daarnaast nader in op het probleem van inflatie en keek naar de betekenis van index-leningen. In ons land toonde de Nederlandsche Bank en Financiën zich grote tegenstanders van index-leningen. Alleen in Engeland waren deze leningen in beperkte maten voor handen. Sindsdien is de indexlening door de introductie in de Verenigde Staten van geïndexeerde treasuries met een scala van looptijden een geaccepteerd instrument. De opzet om het artikel in een Amerikaans tijdschrift te publiceren is nooit gerealiseerd, mede omdat de indexering van pensioenaanspraken een typisch Nederlandse problematiek is. De recente plaatsing van een euro index lening door de Franse staat gaf binnen een beleggingscommissie waarvan ik deel uitmaak een discussie over de rol van dit soort leningen in de portefeuille van een pensioenfonds. Nadat het artikel door een aantal mensen gelezen was en de analyse nog verrassend actueel bleek te zijn kwam het idee op het alsnog te publiceren.
Dit artikel is meer dan 10 jaar geleden geschreven en sluit aan bij twee artikelen in ESB in 1989 en 1990. Beide artikelen waren coproducties met Dr J.M.G. Frijns die de modellering verzorgde. Het was de periode dat binnen het APB de eerste inzichten rond ALM ontwikkeld werden. In het 1989 artikel lieten we zien dat een optimale allocatie onafhankelijk is van het inflatie niveau1 . In het 1990 artikel lieten we zien hoe het systeem van premieaanpassing van invloed is op het gedrag van de dekkingsgraad in de tijd2. Het derde artikel was bedoeld als overzichtsartikel voor de Amerikaanse/Engelse lezer maar ging daarnaast nader in op het probleem van inflatie en keek naar de betekenis van index-leningen. In ons land toonde de Nederlandsche Bank en Financiën zich grote tegenstanders van index-leningen. Alleen in Engeland waren deze leningen in beperkte maten voor handen. Sindsdien is de indexlening door de introductie in de Verenigde Staten van geïndexeerde treasuries met een scala van looptijden een geaccepteerd instrument. De opzet om het artikel in een Amerikaans tijdschrift te publiceren is nooit gerealiseerd, mede omdat de indexering van pensioenaanspraken een typisch Nederlandse problematiek is. De recente plaatsing van een euro index lening door de Franse staat gaf binnen een beleggingscommissie waarvan ik deel uitmaak een discussie over de rol van dit soort leningen in de portefeuille van een pensioenfonds. Nadat het artikel door een aantal mensen gelezen was en de analyse nog verrassend actueel bleek te zijn kwam het idee op het alsnog te publiceren.
Gekozen is voor publicatie in een vrijwel ongewijzigde vorm, maar aangevuld met duidelijk herkenbare commentaren die ingaan op inzichten zoals die de afgelopen jaren ontstaan zijn. In overleg met Jean Frijns is deze bewerking geheel van mijn hand. De commentaren zijn in het nederlands en cursief.
Introduction
Surplus management is a continuous concern to managers of pension funds. One reason may be the fact that there are no clear cut analytical solutions as the world is changing almost continually. Another aspect is the fact that the environment each manager is facing may be different. We felt it might be of interest to the readers of this journal to share some views as they have evolved at a large Dutch pension fund.
The Netherlands might be called a pension country. Almost 25% of the pension assets of the EEC are held in our country. The United Kingdom dominates the scene with about 60%. France and Italy have pay as you go systems for occupational benefits, whereas in Germany companies carry the pension obligation on their own balance sheet; the book reserve method. In the countries mentioned defined benefit schemes are prevalent, although defined contribution schemes are making headway in the United Kingdom. Only the United Kingdom and The Netherlands are faced with the surplus management problem. France and Italy face the more fundamental problem whether they will be able at all to honour the unfunded promises to their people.
Benefit plans
The nature of the obligations is of overriding importance in choosing the approach to surplus management. We know that a tendency exists in the United States and the United Kingdom to move to defined contribution plans and to individual pensions. We feel there are many disadvantages to such an approach.
- Defined contribution plans tend to invest more in fixed income thereby foregoing the long term higher return on equity.
- Defined contribution plans shift the burden of inflation to the individual. This is unreasonable, as the individual cannot possibly hedge against inflation and it will be socially and economically disruptive as large groups in society will face poverty in periods of high inflation.
- Individual pensions face the problem of proper risk coverage for life expectancy and disability.
- Individuals will be exposed to intense marketing efforts. It is questionable whether that process will guarantee balanced decisions or will be cost effective.
Our comment will not change the course of events, but we feel that defined benefit plans, based to a certain extent on solidarity between the participants will remain a valid solution for pension plans.
De recente publicatie van niet-financiële gegevens van pensioenfondsen voor de PVK laat zien dat in een aantal regelingen defined contribution wel sterk gegroeid is, maar in geld spelen ze nog een geringe rol. De bezwaren lijken mij onveranderd te gelden.
 An unstable world
An unstable world
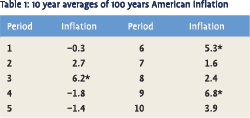
Looking at the character of the obligations we note that defined benefit plans are based on final income and are thus closely linked to inflation. We will not go into detail as to the exact form of indexation but will look only at the impact of inflation in a general sense. Historical analysis shows that inflation is an unstable process. Table 1 presents ten 10 year averages of which three periods, marked with a *, fall outside the two σ interval
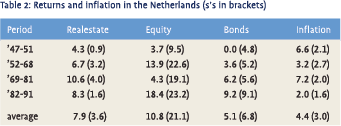 Not only inflation is unstable, so are returns. For The Netherlands the available data cover a shorter period as presented in table 2. An interesting aspect is the inclusion of real estate data of a major insurance company since 1947 3 . These are returns based on appraisal values, the problems of which are well known 4. The periods are chosen in such a way as to create periods with contrasting average inflation levels. Although the long term average returns are in line with conventional wisdom, period returns are not. We find two periods in which real estate outperforms equity, one in which bonds outperforms equity and one in which bonds outperform real estate.
Not only inflation is unstable, so are returns. For The Netherlands the available data cover a shorter period as presented in table 2. An interesting aspect is the inclusion of real estate data of a major insurance company since 1947 3 . These are returns based on appraisal values, the problems of which are well known 4. The periods are chosen in such a way as to create periods with contrasting average inflation levels. Although the long term average returns are in line with conventional wisdom, period returns are not. We find two periods in which real estate outperforms equity, one in which bonds outperforms equity and one in which bonds outperform real estate.
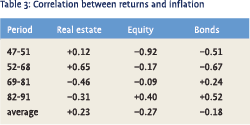 Even more worrying is the fact that the correlations between the asset returns and inflation or liability returns seems to be weak and unstable. Table 3 presents the correlations in The Netherlands. If we had presented returns in real terms, the outcome would have been similar, suggesting that inflation instability and return instability are independent processes.
Even more worrying is the fact that the correlations between the asset returns and inflation or liability returns seems to be weak and unstable. Table 3 presents the correlations in The Netherlands. If we had presented returns in real terms, the outcome would have been similar, suggesting that inflation instability and return instability are independent processes.
At this stage we note that only indexed bonds have the required elasticity of one. If such assets are available complete matching is possible. In other words, a hedge against the instability of inflation is provided. Whether indexed bonds would get a high weighting in the portfolio is a different matter
One provison must be made at this stage. It is the question of time horizon. Asset return characteristics may not be stable over short term periods, they may be close to stable over long periods. Instead of working with annual figures we might work with five or ten year averages as allowed by statement 87 of the FASB or we might employ smoothing assumption in our actuarial calculations. These methods are not commonly used in the Netherlands. This means that the funded ratio will be more volatile.
Deze data zijn natuurlijk gedateerd, maar de vraag is of de laatste 10 jaar zoveel toevoegt. Het is nu wel duidelijk dat aandelenmarkten een uitzonderlijke bubble hebben laten zien die de instabiliteit bevestigt. Het optreden van extreme situaties doet wel de vraag rijzen of we toch niet iets moeten doen met de modellering van mean reversion van asset prijzen. Dat is ingrijpend want er ontstaan dan in feite drie wereldbeelden met aparte regels: een normale wereld, een wereld waarin prijzen te hoog zijn en een wereld waarin prijzen te laag zijn. Het is verhelderend voor de dilemma’s om in ‘The General Theory’ het hoofdstuk 12 ‘The state of longterm expectation’ nog eens door te lezen. De vaste allocaties waarmee nu vaak gewerkt wordt lijkt mij gebaseerd op zoals Keynes dat formuleert: ‘Wordly wisdom teaches that it is better for reputation to fail conventionally than to succeed unconventionally’.
Implication for the analysis
The definition of the problem and the characteristics of asset and liability returns determine the type of analysis. Let us first make three observations.
- The low or negative inflation elasticities of asset returns will have as consequence that returns are dependent upon the inflation level. The question is then whether portfolio composition becomes a function of inflation level and thereby on forecasting of that level. Elsewhere we have shown that the effects on the optimal portfolio are minimal. Inflation is a state of the world with its unescapable consequences.
- In finance risk and return are the generally accepted goal variables. It is questionable whether this is the complete picture. We already mentioned the time horizon and surplus management itself. A longer time horizon means the acceptance of undesirable results on the short term. How far one goes is a matter of judgement and situational aspects. Surplus management means premium adjustments, a sensitive matter to many sponsors, and temporary underfunding, a sensitive matter to supervisory agencies.
- Considering the instability of variables probability calculus will be of little help to project obligations or to predict the behaviour of inflation. Although we will make similar observations as to the return on assets, it is clear that this observation alone has a serious impact. Sometimes, Leibowitz and Kogelman (1991) and Leibowitz, Kogelman and Bader (1992), the portfolio representing the surplus is analyzed in an efficient frontier context 5 . Unstable asset and liability returns make the value of such an analysis doubtful.
These observations lead us away from straight forward optimization or efficient frontier analysis with its specific solutions. We rather prefer to use stochastic simulation to get some feeling for the time path of multiple goals like: premium level, premium fluctuations and the funded ratio. The environment, specially inflation, may be modelled on the historical characteristics taking instability into account. The decision variables are portfolio composition and premium adjustment rules.
In a sense our approach is a next best solution. Straight forward optimization is not possible due to unstable relationships. We can offer also no short term solutions or insights. The best thing to be done is to model the world in a realistic way such that the long term behaviour of decision variables can be better understood.
Deze relativering contrasteert met het huidige gebruik, ook gestimuleerd door de PVK, om ALM te beoordelen op zeer kleine van nature onbetrouwbare overschrijdingskansen, waarbij aan die kansen een buitenproportionele betekenis wordt toegekend. We hebben natuurlijk recent gezien dat deze kansen, die berekend zijn voor een lange termijn op zeer korte termijn volledig achterhaald kunnen zijn. De nadruk zou daarom veel meer moeten liggen op aanpassingsprocessen. In het bijzonder denk ik aan:
- De afbakening van solidariteit tussen deelnemers. Solidariteit is een noodzakelijke voorwaarde voor ons systeem. Er is echter behoefte aan duidelijke afspraken hoe ver die gaat.
- De grenzen van verantwoordelijkheid van de sponsor, zowel in het afromen van surplussen als in het financieren van tekorten.
Onze benadering verschilt ook met modellering die het verleden naar de toekomst doortrekken, zoals de autoregressieve benadering van Ortec. Uit die modellering komt één toekomst, weliswaar als resultante van een groot aantal simulaties. In onze benadering zien we werelden die er steeds anders uitzien, wereldbeelden, waaruit we niet kunnen kiezen.
The analysis
We proceed to model the environment in which the multiple goals have to be satisfied. Our first step is to construct a standard case describing the character of the benefit obligation, the premium adjustment process as well as the inflation and return characteristics. The second step will be to analyze the sensitivity for changes in the inflation modelling, the premium system and the introduction of a new asset class, indexed bonds.
The modelling of returns and inflation
Many researchers have studied inflation elasticities of asset returns. We did our estimations on Dutch data (1947-1990). The bond equations have the interest rate as explanatory variable whereas the equity equation explains the total rate of return. The real estate equation does not produce satisfactory results. A crude approximation is used. Finally a return assumption for indexed bonds is made. Table 4 gives the values for the constant term (denoted by a) and the coefficients of the variables:
r = interest rate
i = inflation rate
i e = expected inflation, based on the auto regressive scheme ie t= 0.85 ie t–1 + 0.15 i t–1
σ = standard deviation of the returns; the standard deviation of i is endogenous
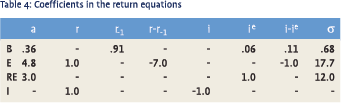 The asset classes considered are: bonds (B), equity (E), real estate (RE) and indexed bonds (I). The correlation between bonds and equity is set at 0.4; between bonds and real estate at 0.3 and between equity and real estate at 0.15.
The asset classes considered are: bonds (B), equity (E), real estate (RE) and indexed bonds (I). The correlation between bonds and equity is set at 0.4; between bonds and real estate at 0.3 and between equity and real estate at 0.15.
As we will not only simulate returns, but also look at the funded ratio we must state how we will value the various asset classes in the balance sheet. Equity and real estate is valued at market value. The return is the change in market value plus the cash return. Bonds are valued at par. The annual return is the average coupon on the portfolio. This is the standard valuation in The Netherlands justified by the fact that a fixed discount rate is used to discount the obligations. The principle of indexed bonds is indexed. Annual return is the base rate plus the indexation.
Deze benadering van waardering past mijns inziens nog steeds als de verplichting met een vaste discontovoet berekend wordt. Met de waardering van vastrentende waarden tegen marktwaarde (noodzakelijk voor performance meting) wordt alleen de actief kant van de balans op marktwaarde gebracht en verhogen we de volatiliteit. Als we dat doen moeten we ook de passief kant op marktwaarde brengen. Dat lijkt de huidige tendens te zijn, wat een aansluiting betekent bij het AngelSaksische systeem. Hoe je dit systeem op een objectieve wijze toepast op aandelen is een andere vraag, nog afgezien van het logische probleem dat de waardering van een verplichting niet afhankelijk kan zijn van de samenstelling van de beleggingen. Dit is het spiegelbeeld van het vermogenskosten probleem van de onderneming.
The specification of the return equations imply that ex post real returns not only depend on the inflation level but also on the dynamics of the inflation process itself. We assume a fairly stable stochastic process:

where ie equals the structural inflation level and z is stochastic term with a standard normal distribution. The values of the parameters are set in such a way that the average inflation is close to the historic level, about 3.8% 6. The return equations together with the inflation process generate the returns used in our modelling
Premium and funded ratio in an uncertain world
Having stressed the uncertainty and instability of returns and inflation, the question becomes how pension funds should balance their multiple goals. To proceed we have to define two factors specific for pension funds; the pension obligation and the premium adjustment process. We consider only the vested rights at any moment in time or the accumulated benefit obligation. The vesting period is minimal. Benefits are accumulated at the rate of 1 3/4 percent per annum based on final pay. The level of funding is expressed by the funded ratio. Supervisory institutions will determine the acceptable bandwidth for the funded ratio. We assume a target of 110. Deviations from that ratio may be corrected by premium adjustments. We start with a moderate adjustment process:

where p = actual premium level; p* = structural or base premium; F = actual funded ratio; F* = the normative funded ratio. The factor (assets/wage sum) is required because the funded ratio is expressed in a percentage of the fund’s assets, whilst the premium is calculated as a percentage of the relevant wage sum. This factor depends on the ‘maturity’ of a pension fund and is usually between 3 and 5. The normative funded ratio F* is set at 110%. It turns out that including a base premium makes the system more stable.
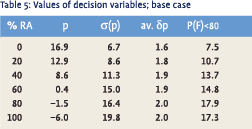 As the stochastic characteristics of the asset returns will influence the behaviour of the system we study a range of asset allocation strategies with varying allocation to bonds and a 80/20 mix of equity and real estate, indicated as real assets (RA). Table 5 presents the results in terms of the decision variables: the premium p, the standard deviation of the premium σ(p), the average premium adjustment δpavg, and the probability of a funded ratio lower than 80%, P(F)<80.
As the stochastic characteristics of the asset returns will influence the behaviour of the system we study a range of asset allocation strategies with varying allocation to bonds and a 80/20 mix of equity and real estate, indicated as real assets (RA). Table 5 presents the results in terms of the decision variables: the premium p, the standard deviation of the premium σ(p), the average premium adjustment δpavg, and the probability of a funded ratio lower than 80%, P(F)<80.
The trade off is obvious. High asset returns generated by real assets reduce the premium level and increase the standard deviation. Negative premium levels are attained by high equity returns, which cause overfunding over long periods. The probability of underfunding is substantial even with so called conservative allocations and does rise quite moderately afterwards. The outcome would suggest fairly high weights for real assets as seen in the United States and the United Kingdom, but not in continental Europe.
De overschrijdingskansen gaan substantieel omlaag als de normatieve dekkingsgraad omhoog wordt gebracht. Tegenwoordig zou een hogere doeldekkingsgraad gekozen worden en zouden ook beleggingsbuffers mee gemodelleerd worden. Een vergelijkbare tabel ontstaat met lagere overschrijdingskansen. Een bijzonder vervelend probleem ontstaat door het feit dat de uitkomsten sterk afhankelijk zijn van de beginstand van de dekkingsgraad. Als we een lange termijn beslissing over de ALM-beslisvariabelen nemen kunnen de beslissingen het volgende jaar, zoals nu gebeurt, achterhaald zijn omdat de nieuwe beginsituatie drastisch verslechterd is. Dit betekent niet alleen dat het hele concept van lange termijn beleid ondergraven wordt, maar de consequentie is ook dat bij lage actuele dekkingsgraden de aandelenweging omlaag gaat en omgekeerd. Dat geeft sterk cyclische effecten die we juist zouden willen vermijden.
De toegestane premiesprongen in de gebruikte orde van grootte zijn relevant wanneer de premie-sprong onderdeel van de jaarlijkse loonruimte is. Dit is het afgelopen jaar natuurlijk actueel geworden.
Het geschetst model en de denkwereld waarbinnen ALM in ons land ontwikkeld is, is gebaseerd op het lange termijn karakter van pensioenfondsen. De aanpassingsprocessen zijn hiervan afgeleid. De PVK heeft de afgelopen jaren een snelle beweging gemaakt naar korte termijn solvabiliteitseisen op basis van liquidatiewaarde. Los van het feit dat dit volledig voorbij gaat aan de aard van de verplichting, betekent dit ook dat een grondige heroverweging van bijsturingsmechanismen zoals hier besproken nodig is. Het lijkt daarbij onvermijdelijk dat het pensioensysteem aangetast gaat worden. Het is verbazingwekkend dat een systeem dat de weerslag is van maatschappelijke consensus diep ingrijpt op het sociale systeem zo makkelijk beïnvloed kan worden door een financiële toezichthouder die zich baseert op zeer discutabele zo niet aantoonbaar onjuiste uitgangspunten.
The sensitivity analysis
We will now study the sensitivity to three factors, inflation, the premium system and the availability of indexed bonds. Starting with inflation, we have modelled a more volatile and unstable process. It is a stochastic process with variable inflation or an ARCH-process, where:

and σ* equals the structural standard deviation. This process generates inflation figures which mimic the past very well. To our surprise the outcome of the simulation produces figures quite similar to those produced in table 5 and they are subsequently not shown.
The fairly high probability of underfunding raises the question whether a faster premium adjustment would alleviate this problem. We reset the parameters in the premium equation such that:

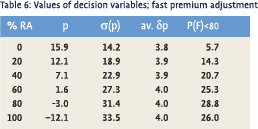 Table 6 presents the results.
Table 6 presents the results.
We see the whole system becoming more volatile.The goal of reducing P(F)<80 is not attained. The probabilities of underfunding are even increased over the whole accepted range of asset allocations. The explanation is that we have structured a cybernetic process. Quick adjustments lead to greater swings just as jerking at the wheel of your car leads to uncontrolled swerves. This result holds important implications for sponsors, pension funds and supervisory agencies.
Het aanpassingsproces is geheel via de premie gestructureerd. Nog relevant is het inzicht dat snelle premie aanpassingen niet optimaal lijken. Tegelijkertijd blijkt dat de doelstelling van een acceptabele dekkingsgraad maar beperkt realiseerbaar is. Het lijkt onvermijdelijk dat in extreme situaties, zoals we nu meemaken, afspraken rond fasering of partiële indexatie gemaakt worden. Dit zou mijns inziens moeten gelden voor actieven, slapers en ingegane pensioenen. Daarbij past een heldere en redelijke afbakeningen van solidariteit. De laatste paragraaf van het artikel loopt al op deze noodzaak vooruit. Dit was destijds een zeer gevaarlijke uitspraak voor een directielid van het ABP.
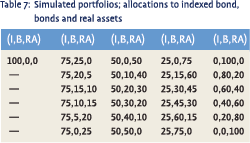 Finally we are interested in the impact of the availability of indexed bonds. One would expect that with more complete markets it would be possible to reach higher efficiency levels. Adding an asset class explodes the number of possible allocations. Table 7 presents the allocations, which were analysed. Note that we use the same fractions as before for the allocation to bonds and real assets for the part not allocated to indexed bonds.
Finally we are interested in the impact of the availability of indexed bonds. One would expect that with more complete markets it would be possible to reach higher efficiency levels. Adding an asset class explodes the number of possible allocations. Table 7 presents the allocations, which were analysed. Note that we use the same fractions as before for the allocation to bonds and real assets for the part not allocated to indexed bonds.
From the outcome of the simulations we may derive an efficient set taking the premium and its standard deviation as determining variables. It is the envelope of the individual curves for each allocation to indexed bonds. The results are presented in table 8. The shaded cells are the efficient portfolios.
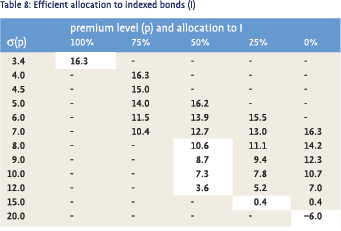 As expected adding the missing asset produces more efficient portfolios. A previously nonexistent range of low risk portfolios is added. Only in the high risk/low premium range portfolios with I=0% are efficient or close to efficient.
As expected adding the missing asset produces more efficient portfolios. A previously nonexistent range of low risk portfolios is added. Only in the high risk/low premium range portfolios with I=0% are efficient or close to efficient.
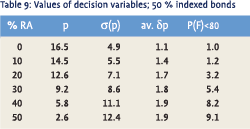
Taking he mid range of I = 50% as an example, we may get an idea of the possible benefits in terms of our decision variables. Table 9 presents the results. Real assets (RA) are still defined as equity and real estate in the proportion 80/20.
Comparing the results with table 5 confirms our earlier conclusion. Given a certain level for σ(p) it is possible to achieve a lower premium and a significantly lower probability of underfunding. The cost to society of the general unavailability of indexed bonds must be substantial indeed. It continues to amaze us that so few economic agents with indexed assets, including governments, issue indexed debt. For them the same would apply as for pension fonds; lower cost and less risk.
 Inmiddels is in de Verenigde Staten een scala van indexed treasury bonds geintroduceerd. In het eurogebied is een schoorvoetend begin gemaakt. De analyse laat duidelijk zien dat indexleningen thuis horen in de portefeuille van pensioenfondsen tenzij men kiest voor zeer hoge aandelen allocaties. Enerzijds is een gebied met lager risico bereikbaar terwijl anderzijds in het middengebied van risico een hele reeks van meer efficiente portefeuilles ontstaat. Absoluut is het risico trouwens onderschat omdat geen rekening is gehouden met reële loonstijgingen.
Inmiddels is in de Verenigde Staten een scala van indexed treasury bonds geintroduceerd. In het eurogebied is een schoorvoetend begin gemaakt. De analyse laat duidelijk zien dat indexleningen thuis horen in de portefeuille van pensioenfondsen tenzij men kiest voor zeer hoge aandelen allocaties. Enerzijds is een gebied met lager risico bereikbaar terwijl anderzijds in het middengebied van risico een hele reeks van meer efficiente portefeuilles ontstaat. Absoluut is het risico trouwens onderschat omdat geen rekening is gehouden met reële loonstijgingen.
Een index-lening is het meest effectief als de indexering dezelfde is als de indexering van de verplichtingen. Nederland kent via de woningcorporatie een grote geïnstitutionaliseerde met inflatie geïndexeerde huurstroom. Het blijft relevant de instrumenten te ontwikkelen om deze te transformeren naar een geïndexeerde belegging voor pensioenfondsen die grootschalige toepassing mogelijk maken.
Time horizon and solidarity
Our analysis must now return to the question of time horizon and solidarity. It is obvious that an individual will run into serious financial problems in periods of underfunding, particularly so if he has to liquidate his equity portfolio in depressed equity markets. As we saw this danger will cause him to avoid equities thereby foregoing the higher long term return. Defined contribution systems, which do not allow for temporary deficits have this unpleasant side effect. On the other hand defined benefit pension plans, which have to pass an annual test for a funded ratio are also in trouble. However if plans would be allowed to smooth their premium and funded ratio, they might bridge periods with unfavourable return characteristics. Of course the sponsors of such plans should be financially strong. A long-term time horizon and some measure of solidarity would be required. This brings us back to our introduction in which we indicated the advantages of that approach. We feel that the public sector is an area well suited to this approach. In situations where underfunding is not possible the same result might be attained by other means. For example indexation could be made contingent on the availability of assets combined with an obligation to increase premiums over time to finance the temporarily postponed vesting rights.
Notes
- Frijns, J.M.G. en J.H.W. Goslings, Matching voor het Pensioenbedrijf, 6 september 1989, pp. 868-871.
- Frijns, J.M.G. en J.H.W. Goslings, Premiesystemen en Beleggingssamenstelling, ESB 5 december 1990, pp. 1168- 1172.
- Eichholtz P.M.A. en N. Tates, Investment in real estate in the Netherlands, January 1993, ESB 3895.
- See e.g. Ross S.A., R.C. Zisler, Risk and Return in Real Estate. Journal of Real Estate Finance and Economics, 4, 1991 and Firstenberg P.M., S.A. Ross and R. Zisler: Real Estate: The Whole Story. The Journal of Portfolio Management, Spring 1988.
- M.L. Leibowitz and S. Kogelman, Asset Allocation under shortfall Constraints, Winter 1991 and M. L. Leibowitz, S. Kogelman and L.N. Bader, Journal of Portfolio Management, Winter 1992.
- The specification also assures that the lagged weights of i e in the interest equation equal the weight of ie in the long-term equilibrium for the interest rate r = 4 + 0.67 ie .
in VBA Journaal door Dr J.H.W. Goslings
